Week 7 Entry - Matrices

The Matrix

Evolving from much of the same methods used in vector math, a matrix for our purposes will be utilized as a collection of multi-dimensional vectors. These vectors will more specifically represent columns of basis vectors. By organizing our matrices into 4-dimensional constructs (4 rows by 4 columns), we can transform matrix and vector-based objects in ways of scaling, rotating, translating, and projection. Conceptually, the result of applying a matrix manipulation is to answer the question "where would my matrix end up once this new matrix, based on a different set of basis vectors, is applied?"

Important notes regarding matrix manipulation and combination include matrix multiplication is associative but not commutative, operations such as scaling and rotating are relative to the origin and not necessarily the center of the object at the time of transformation, and the combination of multiple matrices (through multiplication) must be performed from right to left. For projection through matrices, we have the choice of two methods: orthographic projection and perspective projection. Orthographic projection results in parallel lines in the geometry space being represented still as parallel, with proportions maintained, in the projected image. Perspective projection results in a more realistic representation of geometry and space by having lines converge to a point (the eye or camera) as opposed to parallel toward a perpendicular plane.

Should Have Taken Linear Algebra

Until just over one week since today, I had considered the fact that I'd not been required to venture into a linear algebra class as a blessing in disguise. That, most certainly, is no longer the case. The content from the slides, as well as the visual guides and representations provided by 3Blue1Brown, helped tremendously in getting into the matrix mindset. That being said, however, I had forgotten much about matrix methods and how exactly they were to be properly combined.

This became quite clear after spending a significant amount of time on the '.multiply(Matrix4Object)' function. On top of trying to make the code clean and clear, I was simultaneously re-learning how to multiply a matrix on paper. Ideally, I would have had the latter logic figured out before coding, but I let my ignorant confidence get the best of me. This resulted in too much time spent stepping through my code, writing down the variable values and matrix index results from one iteration at a time, and eventually scrapping most of the code after I recognized that there was a mathematical misunderstanding I was holding onto.

Lesson to be learned: my code, and time spent coding, benefit greatly when I spend an appropriate amount of energy being sure that I understand how to apply new concepts outside of programming. Having this concrete understanding will not only help me in creating functional code but also in being confident in my fundamental knowledge for applying these concepts in different, creative, but predictable ways.

Freeze Frames - Coalescence of Confusion

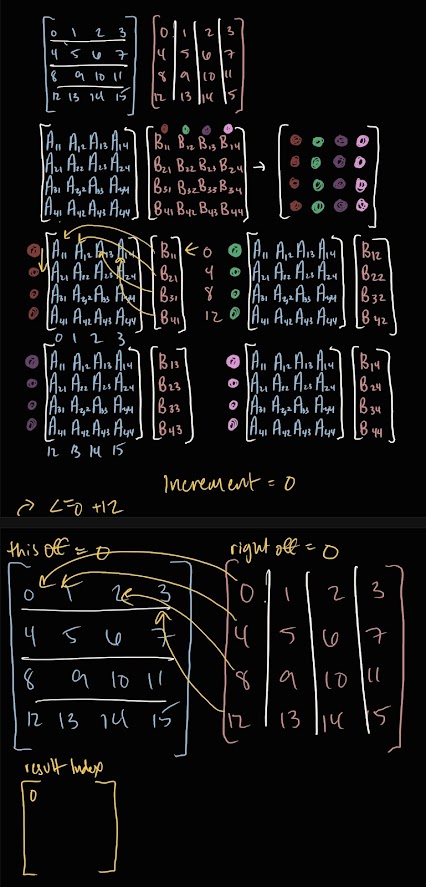
Some would call these the scribbles of someone who's lost their mind...
I would be hard-pressed to disagree.

moonMatrix.multiply(earthWorldMatrix.clone())

.multiply(new Matrix4().makeRotationZ(moonRotationAngle))

.multiply(new Matrix4().makeTranslation(offsetFromEarth));